InstructG2I: Synthesizing Images from Multimodal Attributed Graphs

Bowen Jin1, Ziqi Pang1, Bingjun Guo1, Yu-xiong Wang1, Jiaxuan You1, Jiawei Han1
1University of Illinois at Urbana-Champaign
Paper arXiv Code Data Model
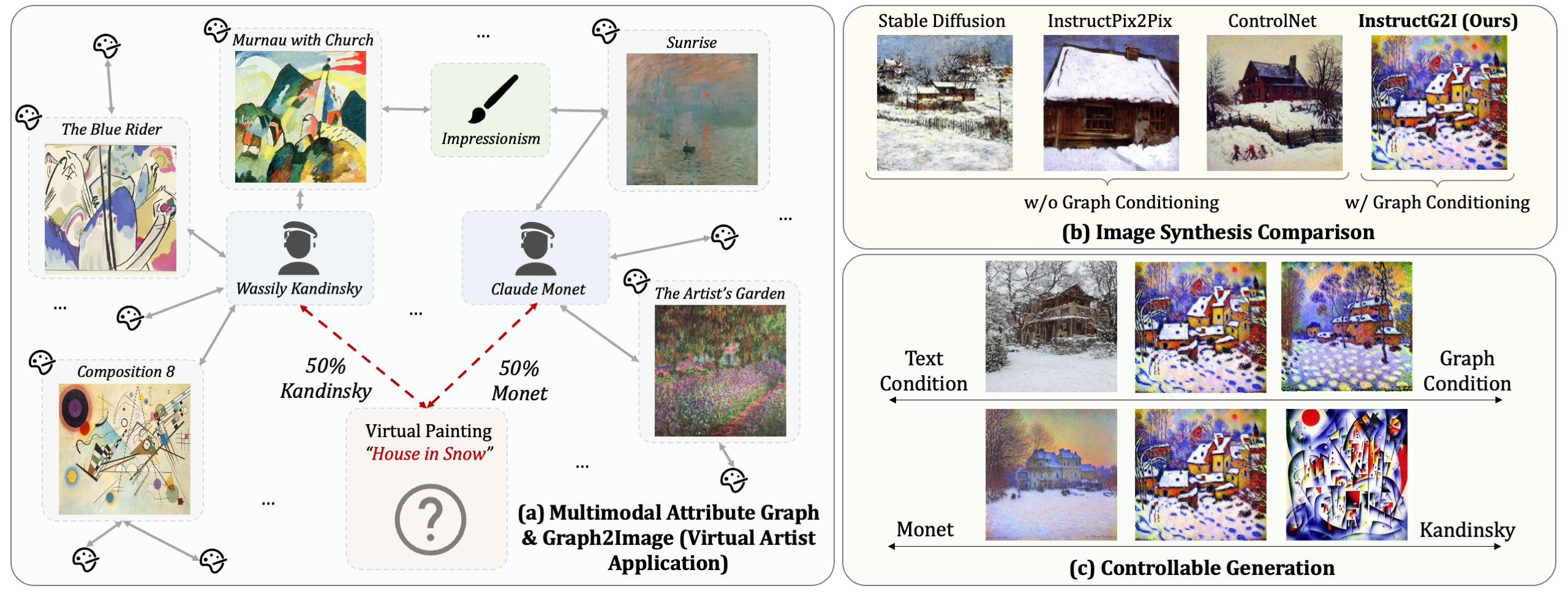
Teaser Image

We propose a new task Graph2Image featuring image synthesis by conditioning on graph information and introduce a novel graph-conditioned diffusion model called InstructG2I to tackle this problem.

Abstract

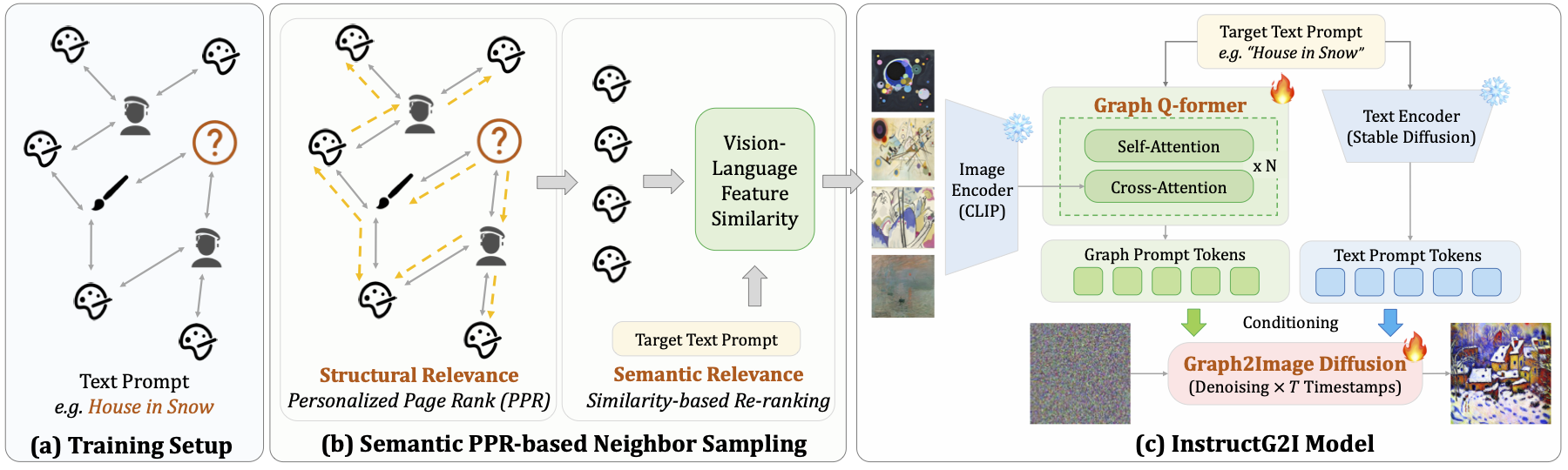
In this paper, we approach an overlooked yet critical task Graph2Image: generating images from multimodal attributed graphs (MMAGs). This task poses significant challenges due to the explosion in graph size, dependencies among graph entities, and the need for controllability in graph conditions. To address these challenges, we propose a graph context-conditioned diffusion model called InstructG2I. InstructG2I first exploits the graph structure and multimodal information to conduct informative neighbor sampling by combining personalized page rank and re-ranking based on vision-language features. Then, a Graph-QFormer encoder adaptively encodes the graph nodes into an auxiliary set of graph prompts to guide the denoising process of diffusion. Finally, we propose graph classifier-free guidance, enabling controllable generation by varying the strength of graph guidance and multiple connected edges to a node. Extensive experiments conducted on three datasets from different domains demonstrate the effectiveness and controllability of our approach.

Model Architecture

Model Architecture
The overall framework of InstructG2I. (a) Given a target node with a text prompt (e.g., House in Snow) in a Multimodal Attributed Graph (MMAG) for which we want to generate an image, (b) we first perform semantic PPR-based neighbor sampling, which involves structure- aware personalized PageRank and semantic-aware similarity-based reranking to sample informative neighboring nodes in the graph. (c) These neighboring nodes are then inputted into a Graph-QFormer, encoded by multiple self-attention and cross-attention layers, represented as graph tokens and used to guide the denoising process of the diffusion model, together with text prompt tokens.

Controllable Generation

In our task, the score network \(\hat{\epsilon}_\theta(\mathbf{z}_t, c_G, c_T)\) is conditioned on both text \(c_T=d_i\) and the graph condition \(c_G\). We compose the score estimates from these two conditions and introduce two guidance scales, \(s_T\) and \(s_G\), to control the contribution strength of \(c_T\) and \(c_G\) to the generated samples respectively. Our modified score estimation function is: \[ \hat{\epsilon}_\theta(\mathbf{z}_t, c_G, c_T) = {\epsilon}_\theta(\mathbf{z}_t, \varnothing, \varnothing) + s_T \cdot ({\epsilon}_\theta(\mathbf{z}_t, \varnothing, c_T) - {\epsilon}_\theta(\mathbf{z}_t, \varnothing, \varnothing)) \notag \\ + s_G \cdot ({\epsilon}_\theta(\mathbf{z}_t, c_G, c_T) - {\epsilon}_\theta(\mathbf{z}_t, \varnothing, c_T)).\label{eq:cfg1} \] For cases requiring fine-grained control over multiple graph conditions (i.e., different edges), we extend the formula as follows: \[ \hat{\epsilon}_\theta(\mathbf{z}_t, c_G, c_T) = {\epsilon}_\theta(\mathbf{z}_t, \varnothing, \varnothing) + s_T \cdot ({\epsilon}_\theta(\mathbf{z}_t, \varnothing, c_T) - {\epsilon}_\theta(\mathbf{z}_t, \varnothing, \varnothing)) \notag \\ + \sum s^{(k)}_G \cdot ({\epsilon}_\theta(\mathbf{z}_t, c^{(k)}_G, c_T) - {\epsilon}_\theta(\mathbf{z}_t, \varnothing, c_T)),\label{eq:cfg2} \] where \(c^{(k)}_G\) is the \(k\)-th graph condition. For example, to create an artwork that combines the styles of Monet and Van Gogh, the neighboring artworks by Monet and Van Gogh on the graph would be \(c^{(1)}_G\) and \(c^{(2)}_G\), respectively.

Qualitative Evaluation

Qualitative Evaluation
Qualitative evaluation. Our method exhibits better consistency with the ground truth by better utilizing the graph information from neighboring nodes (“Sampled Neighbors” in the figure).

Text and Graph Guidance Balance

Qualitative Evaluation 1
The ability of InstructG2I to balance text guidance and graph guidance.

Multiple Graph Guidance Study

Qualitative Evaluation 2
Study of multiple graph guidance. Generated artworks with the input text prompt “a man playing piano” conditioned on single or multiple graph guidance (styles of “Picasso” and “Courbet”).

Virtual Artist

Virtual Artist
Virtual Artist (We can combine the styles of any artists of any number). In this example, we generate pictures combining the style of Pablo Picasso and my little brother.

BibTeX

@article{jin2024instructg2i,
  title={InstructG2I: Synthesizing Images from Multimodal Attributed Graphs},
  author={Jin, Bowen and Pang, Ziqi and Guo, Bingjun and Wang, Yu-Xiong and You, Jiaxuan and Han, Jiawei},
  journal={arXiv preprint arXiv:2410.07157},
  year={2024}
}